WHAT: w-tinylfu是什么?
w-tinylfu = window tiny LFU
实际是一种缓存置换算法,直译过来大概是带一个窗口的tiny版本的LFU实现;
主要用三段LRU,一个布隆过滤器、一个cm-sketch计数器,兼顾了LFU和LRU的优点。
大致思想上类似于别的分段lru算法(例如mysql中buffer pool的lru链表,5/8存young page,3/8存old page)。
背景
学术界:
来自论文:https://arxiv.org/pdf/1512.00727.pdf
工业界:
实现:java中的caffeine缓存就用的是w-tinylfu算法。
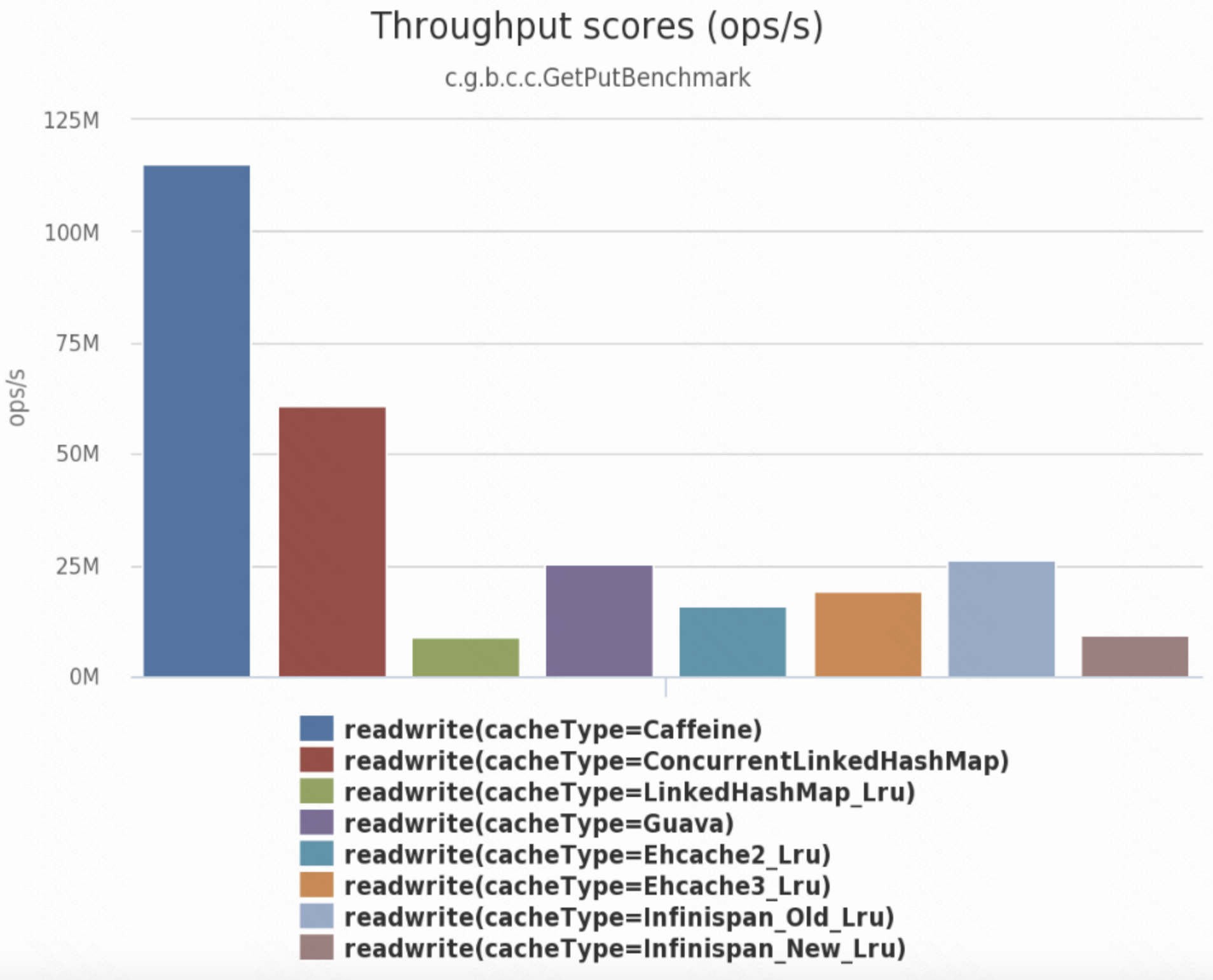
当然这里caffeine的性能好除了w-tinylfu算法的贡献,还有其他很多优化比如结合了disruptor(RingBuffer)、时间轮;
WHEN: 什么时候使用w-tinylfu算法
缓存置换算法也不是银弹,也需要匹配它适合的某些分布workload。
即使是匹配的分布的workload,实际参数也要和workload匹配才能达到最好性能。
w-tinylfu算法适合的工作负载的大概特征:
- 静态的偏态分布;(分布规律不怎么变化)
- 有一定动态变化(不能变化得太快太剧烈)的分布、包括有一定突发流量的偏态分布,例如偶有突发流量的zipf分布。
比较合适的:
benchmark中测试的workload比较合适的包括:
youtube、维基百科、数据库访问、windows文件系统、搜索引擎;
不太合适的:
OLTP中的磁盘访问: 轨迹实际是顺序访问的升序队列中散布一些随机访问,这对于w-tinylfu来说不太适配。
具体的调参涉及到算法内部细节,因此最后在调优章节再展开。
HOW: w-tinylfu具体是怎么做的
目标、要解决的问题
1。提高缓存命中率;
现有方案的缺点:LFU: 数据访问模式有变化时(例如有突发流量),LFU较迟钝,始终缓存早先访问多的数据;LRU: 不能记忆历史的访问规律,高频访问key并不一定能缓存到。
2。降低内存消耗;
现有方案的缺点:LFU: 需要给每个key维护频率信息(PLFU记录所有key的频率;WLFU则记录当前缓存中key的频率),需要巨大的内存消耗。
总之,w-tinylfu需要以较低的内存消耗达到高命中率。
架构、解决方案
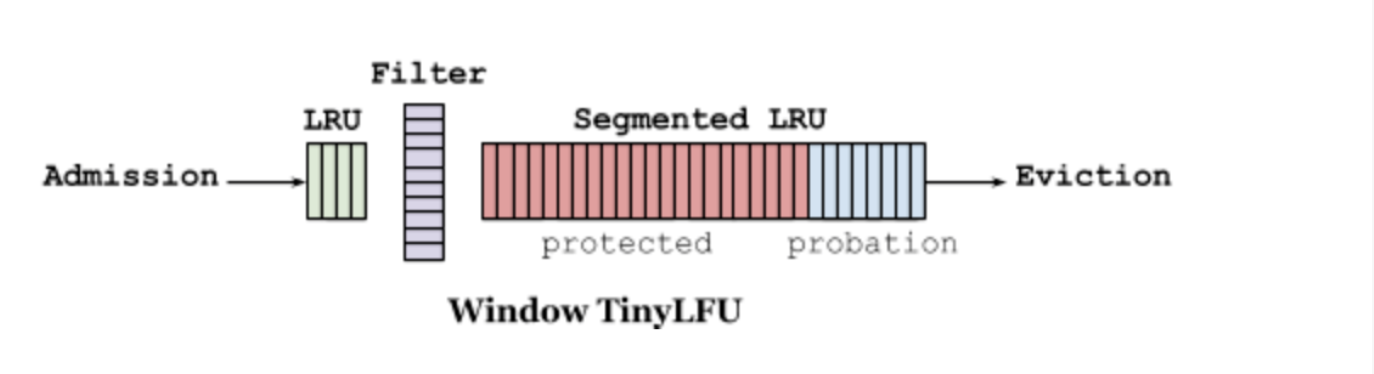
如上图所示:
1。LRU: 最左边是一个普通的LRU窗口,默认占1%的空间,负责处理突发流量的情况;
2。filter: 第2个组件是一个布隆过滤器,作为看门人,负责阻挡长尾的低频访问、避免纳入计数器;
3。Segmented LRU: 第3个组件是分段LRU,分为两段:
(1)protected: 受保护区,占80%,存放访问次数>1的数据;
(2)probation: 缓刑区域, 占20%,存放访问次数=1的数据;(淘汰备选)
按我理解,其实还应该有一个组件负责统计频次,但论文中没有相应的图。
这里按我理解直接补上:
4。CM-Sketch: 近似统计频次。这里类似于WLFU,只记录当前缓存中有出现的key的频率,使用count min sketch算法。
近似统计频次算法,因此有一定错误率,但也极大节省了内存。
节省内存:CM-Sketch算法近似统计
count min sketch算法,类似于计数版本的布隆过滤器,把布隆过滤器原来标记是否存在的0\1改成能存更多值的计数器。
由于考虑到实际workload中常见的是长尾分布,因此计数器实际位数不多,默认只有4位,也就是默认大部分数据访问频次在15次以内。
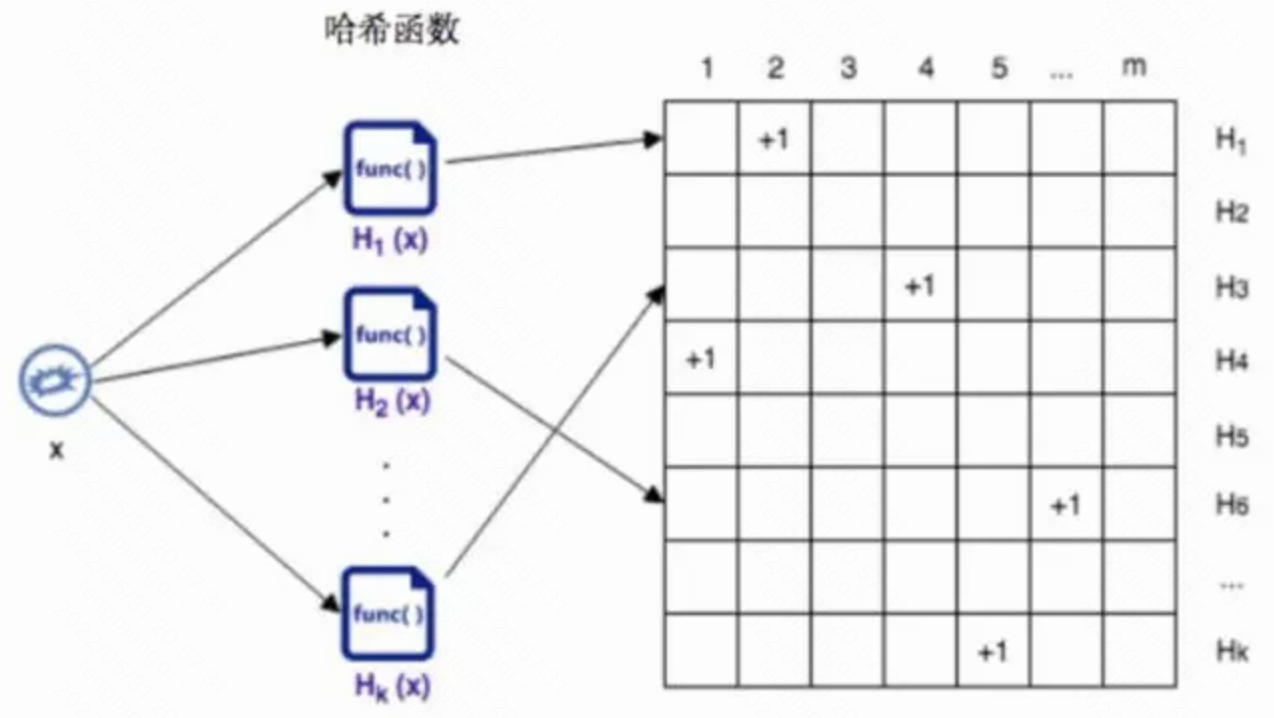
CM-SKetch使用多个哈希函数(或者1个哈希函数和多个种子)和多个计数器来记录访问的次数。
实际读的时候取所有计数器里最小的一个,因此其他计数器的值其实就没什么用了。
而且由于哈希碰撞,有一定的概率频次的估计会偏大,(但是不会偏小)
因此实际每个key的统计频次增加的时候,可以只增大当前最小的计数器。
调参
假如处理的数据规模是n,希望估计值落在[实际值, 实际值+ a*n]范围的概率是1-b;
则:
1.计数器数量为: e/a 的上界;
2.哈希函数的数量为: ln(1/b) 的上界;
例如当n=10^6时,如果我们希望估计值落在实际值, 实际值+ 2000范围的概率是99%,
则:
- 计数器数量为: e/0.002 的上界 = 1360;
- 哈希函数的数量为: ln(1/0.01) 的上界 = 5;
当计数器占4bit,则整个计数组件占空间 = 136054 bit= 约3.5KB。
动态访问模式(访问key的分布变化):Freshness Mechanism(保鲜机制)
统计新增key到CM-Sketch计数器的次数w,一旦w达到阈值W的大小时,进行reset操作。
reset操作实际有两方面:
(1)将所有计数器的值减半(可以通过简单的>>和&0x77操作来实现);
// 副作用:可能除不尽,计数误差+1。
(2)将看门人的bloom filter清空。
// 副作用: 计数误差+1;
节省内存、长尾分布优化:Doorkeeper(看门人)机制
解决的问题:长尾分布。现实时间的访问轨迹大多符合长尾效应的偏态分布,也就是大部分访问key只访问很少次数,比如1次。
如果这些流量也纳入近似统计用的CM-Sketch,就会极大扩大本来就有概率发生的哈希碰撞,从而影响性能。
如果要维持出错概率不上升,只能增大计数器的槽位(哈希表的格数),增加内存消耗。
因此这里的DoorKeeper机制,就是在近似统计组件前面增加一个防护存储: 一个布隆过滤器。
在纳入CM-Sketch之前,首先要先检查一下在不在filter里面:
(1)如果有: 说明之前可能有访问过,通过,纳入计数器;
(1)如果没有: 说明之前没有访问过,拒绝写入计数器;但写入filter记录下来。// 下次如果再访问则能通过。
通过这种看门人机制,可以阻拦大部分只访问1次的key,避免将大量资源消耗在这些key上面。
读写流程
读
从lru或者segment lru部分读取,然后增加计数器的值即可。
可能导致probation中的key升级到protected。
写
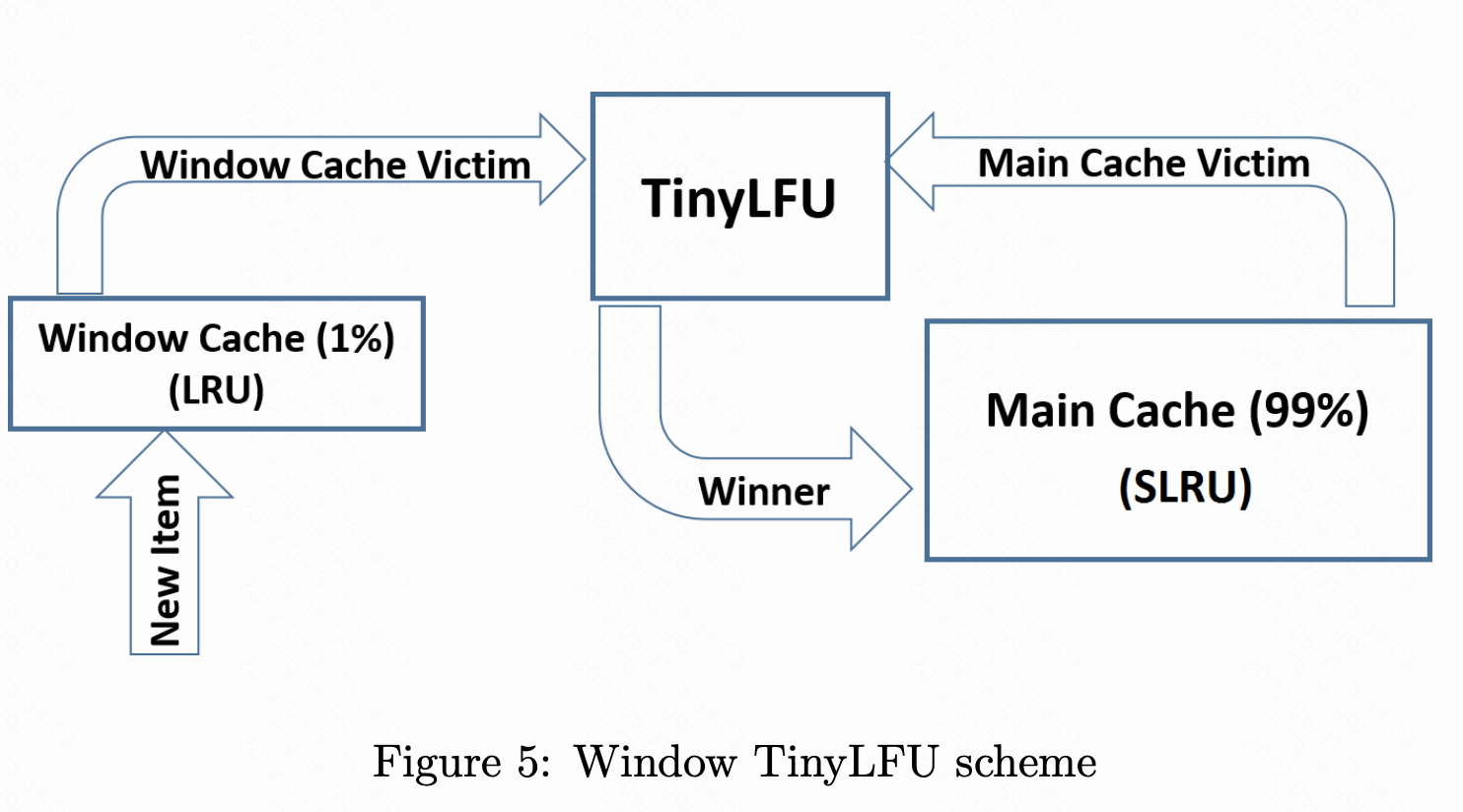
如上图所示,新item插入的时候,首先进入lru;
如何如果lru满了,淘汰者和分段lru的淘汰者pk,(根据近似计数器中的频次)。
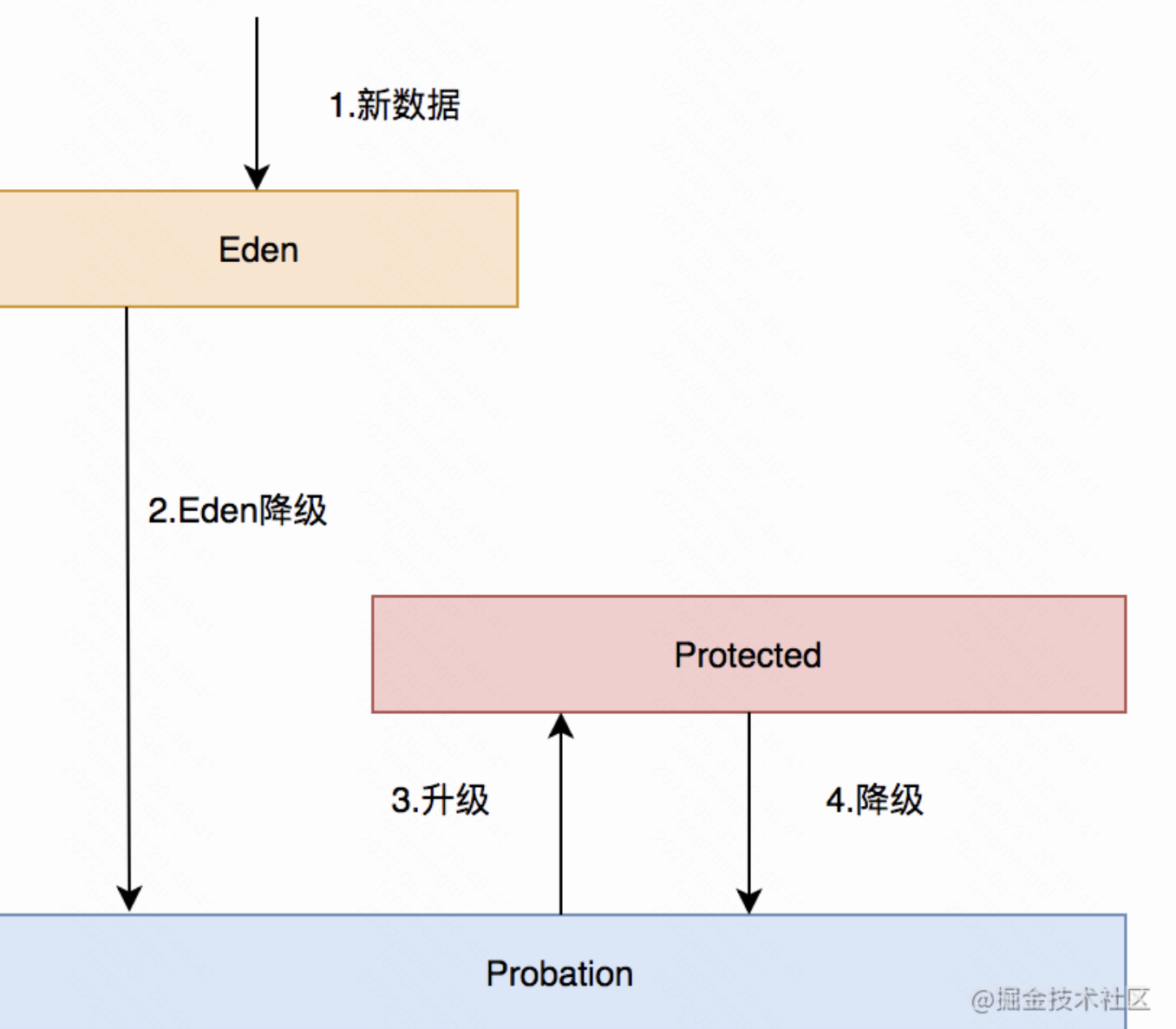
而在分段lru中,probation缓刑区中访问则升到protected区。(反之protected的淘汰者降级到probation)
调优参数
回顾各个组件:
1。LRU: 默认占1%的空间,负责处理突发流量的情况;
因此如果实际突发流量占不止1%的内存空间,可能需要调大这部分;(反之亦然)
2。filter: 布隆过滤器; 只拦了访问次数=1的,因此如果长尾是2次,则可能要调整这部分。
3。Segmented LRU:
(1)protected: 受保护区,占80%,存放访问次数>1的数据;
(2)probation: 缓刑区域, 占20%,存放访问次数=1的数据;(淘汰备选)
4。CM-Sketch: 默认是4位计数器,最大15次。隐含假设是大部分访问<15次,因此如果这个假设不成立,也要调整这部分。
参考资料
论文: https://arxiv.org/pdf/1512.00727.pdf
https://xuzhijvn.github.io/zh-cn/posts/cs/other/caffeine/
https://jishuin.proginn.com/p/763bfbd34443
cm-sketch算法: https://zhuanlan.zhihu.com/p/369981005
