数据结构与算法

2-3树与红黑树

2-3树与红黑树

参考资料：
2-3树：
http://blog.jobbole.com/79307/
红黑树：
http://blog.jobbole.com/79309/

背景

2-3树和红黑树都是一种平衡查找树。其中红黑树是在2-3树的基础上，对于实现进行了简化，代价是逻辑上（表现图）增加了直接理解的难度。换句话说就是:

  • 2-3树理解起来简单，实现起来代码比较麻烦(其实也可以实现);
  • 红黑树理解起来稍微曲折，实现起来代码非常简单/简洁,如果用递归实现还非常优雅。

因此我们应该先学2-3树，理解以后，带着简单理解去学红黑树的实现。上述参考资料里的两个链接对于两者的介绍非常值得一看。

2-3树

定义

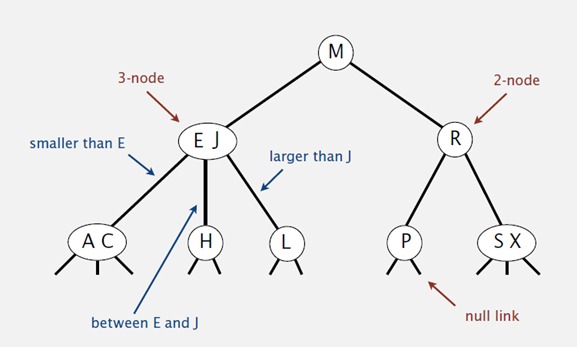
2-3树意思就是树里有两种节点:
2-node: 保存1个key,左右2个子节点;
3-node: 保存2个key,左中右3个子节点。

和二叉查找树类似,如果中序遍历一个2-3树,可以得到一个排好序的序列。
在一个完全平衡的2-3树中,根节点到每一个叶节点距离相同.

平衡性:

直观上理解: 由于2-3树的3-node具有缓冲作用,而且它的分裂逻辑可以将不平衡因子传递到父节点(还可以继续),最终消除;
严谨证明: 还没找到相关论文,理论上它与AA树等价,所以可以按left-leaning red-black tree/LLRB的证明来完成。

查找

和B树类似,按key跳转子节点查找就好了.

插入

往2-node节点插入

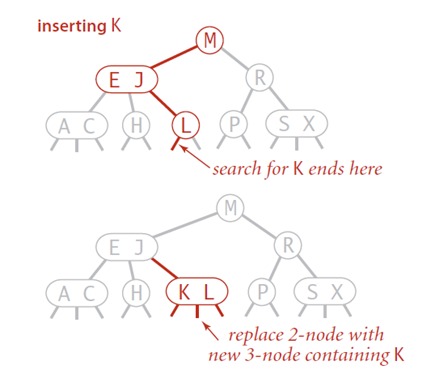
插入K,把2-node变成3-node。

往3-node节点插入

1. 只有一个3-node节点

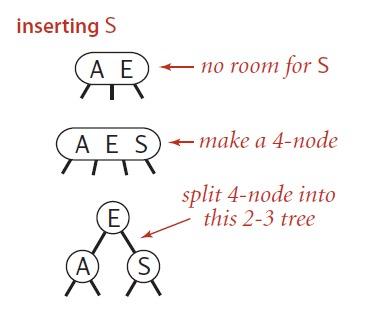
插入S,把3-node变成4-node,把4-node分裂成3个2-node,中间key拉升做根节点.（无法向上传导,根分裂,高度+1）

2. 父节点是2-node,节点是3-node

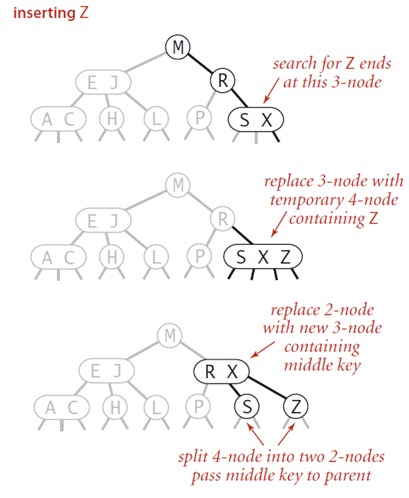
插入Z:

  1. 把3-node变成4-node;
  2. 把中间key往上扔,传递给父节点;
  3. 父节点从2-node=>3-node。

3. 父节点是3-node,节点是3-node

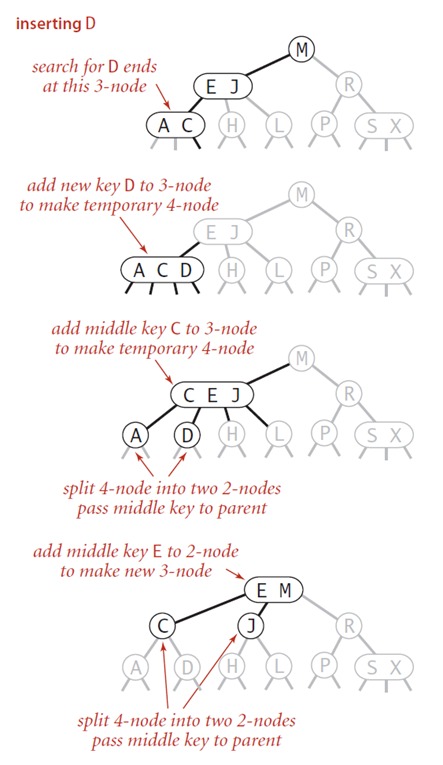
思路和之前相似,把中间元素往上传导,直到遇到父节点是2-node的。
如果连根节点也是3-node，就进行根节点分裂，高度+1。

性能

最坏情况,所有节点都是2-node,因此最坏时间复杂度为O(logN).
最好情况,所有节点都是3-node,因此最好时间复杂度为O(log3N)=0.631logN.

红黑树

(这里其实是left-leaning red-black tree/LLRB)
2-3树中有3-node，红黑树则是将其全部转化成二叉树来实现。
参考资料2中同时出现红色节点与红色连线,容易引起混淆. 这里统一定义一下, 红色本质上是指节点,红黑信息实现上存放在红子节点中. 之所以有红色连线,主要是为了在图里画,可以更清晰得看出有两个红子节点的父节点.

下文中:

  1. 图中: 以红色连线表示子节点是红节点;️
  2. 实现中: 红色信息存放在子节点中. （并不会存指向父节点的指针）

具体实现:

1
2
3
4
5
6
7
8
9
10
11
class Node
{
    public Node Left { get; set; } // 左子
    public Node Right { get; set; } // 右子
    public TKey Key { get; set; } // key
    public TValue Value { get; set; } // 数据
    public int Number { get; set; } // 当前子树的size,总共有多少节点 
    
    // 当前节点是红还是黑
    public bool Color { get; set; }  
}

定义:

1
2
3
1. 所有节点分为红节点和黑节点;
2. 表现图中一个红节点的画法: 把它和父节点之间的连线画成红色。
(看图的时候,一条红线:子节点是红节点)

规则:

1
2
3
4
1. 所有节点,只有左子节点可以是红节点, 右子节点只能是黑;(通过旋转保证)
2. 红色节点不能相连; // 父节点红色,子节点不能也红色
3. 不能左右都是红节点. // 左右子节点不能都是红色
(2，3两个规则,图上看就是一个节点不能有两个红色连线)

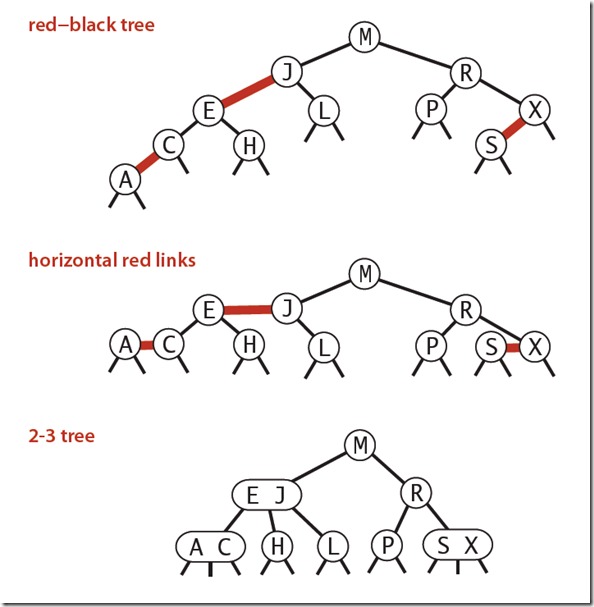
如上图所示，红黑树其实是2-3树的另一种表现形式。将红黑树的红色连线水平绘制，就可以把水平的两个节点整体看作一个3-node.
从实现上看，也就是把节点和它的红子节点看作一个3-node。
从这个思路来看,也就能理解上述的3条规则了, 如果违反了任意一条,都会导致节点与其红子节点合并成一个整体来看待的时候, 变成4-node甚至5-node更多.
只有满足所有规则, 才能保证合并来看的时候最多是一个3-node。

查找

由于本质上还是二叉查找树,查找的代码与普通二叉查找树一样.
只不过由于比较平衡,性能有保障。
(如果把红黑树看作2-3树的话,查找过程的差别就在于遇到3-node的时候,先找的是最左的key,然后通过红子节点查找了中间key。)

平衡化

为了维持上文中的规则，也为了红黑树保持平衡,保障性能,需要进行一些平衡操作。

旋转

左旋: 输入父节点;
右旋: 输入父节点.

左旋

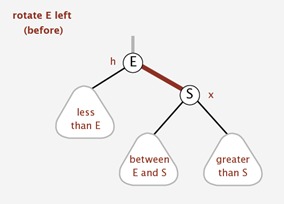
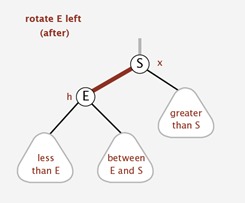
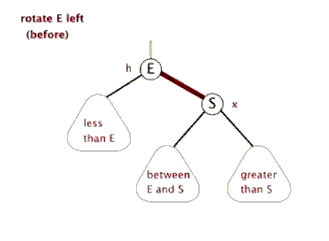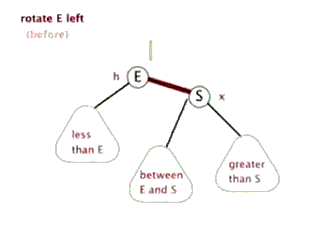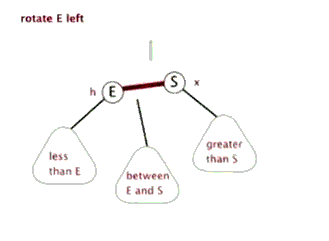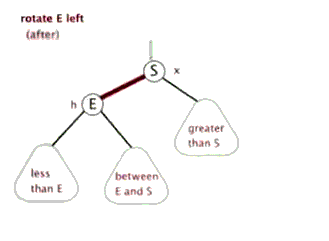
左旋实现:

1
2
3
4
5
6
7
8
9
10
11
12
//左旋转
private Node RotateLeft(Node h)// 输入父节点
{
    Node x = h.Right;
    //将x的左节点复制给h右节点
    h.Right = x.Left;
    //将h复制给x右节点
    x.Left = h;
    x.Color = h.Color;
    h.Color = RED;
    return x;
}

注意: 子节点继承父节点的颜色.
父节点变为红色。

右旋

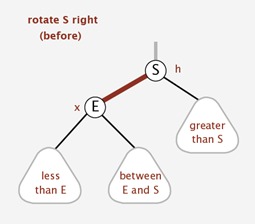
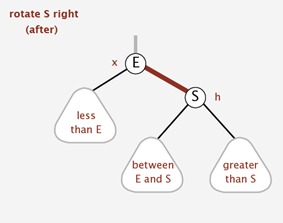
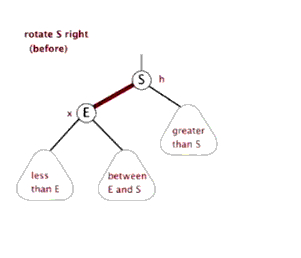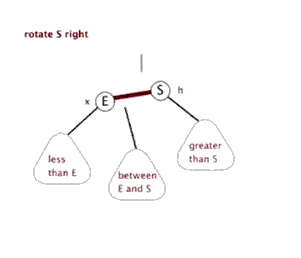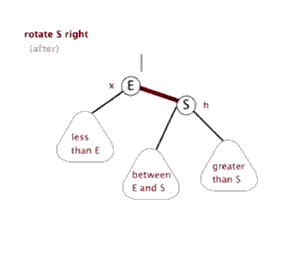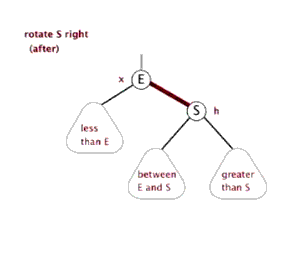
右旋实现:

1
2
3
4
5
6
7
8
9
10
11
//右旋转
private Node RotateRight(Node h)// 输入父节点
{
    Node x = h.Left;
    h.Left = x.Right;
    x.Right = h;

    x.Color = h.Color;
    h.Color = RED;
    return x;
}

注意: 子节点继承父节点的颜色.
父节点变为红色。

颜色反转

如果违反规则2，也就是两个子节点都是红色节点,也需要调整/平衡化.如下图所示的话,其实就是把父节点变成红色，两个子节点变成黑色. 很简单。

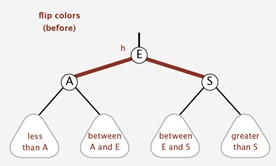
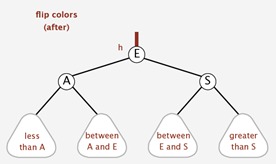
插入

往2-node底部插入

规则:

1
新插入的节点标记为红色.

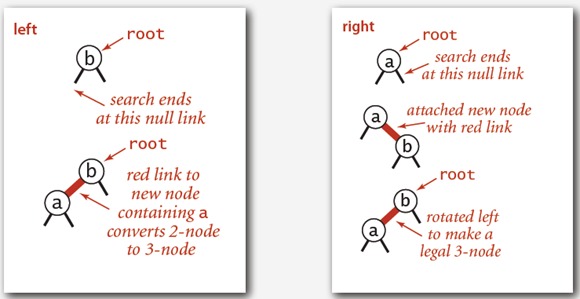
左图不需要额外操作;
右图需要一次左旋.

往3-node底部插入

  1. 往只有两个节点的树中插入: （注意形状一定是左偏的）
    规则:
    1
    新插入的节点标记为红色.
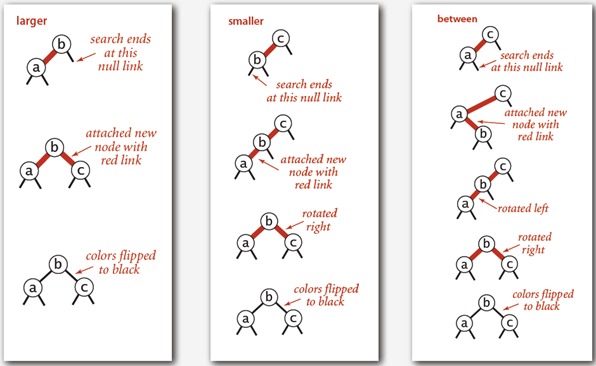    左图需要1次颜色反转;
    中图需要1次右旋,1次颜色反转;
    右图需要1次左旋,1次右旋,1次颜色反转.

简单总结一下平衡化的技巧如下:(按顺序检查,每次调整后回到1从头重复检查)

  1. 如果左右都是红,用颜色反转;
  2. 如果右子是红,左旋;
  3. 如果连续两个左子是红,(父子都是红节点),右旋,然后颜色反转.

更多案例:

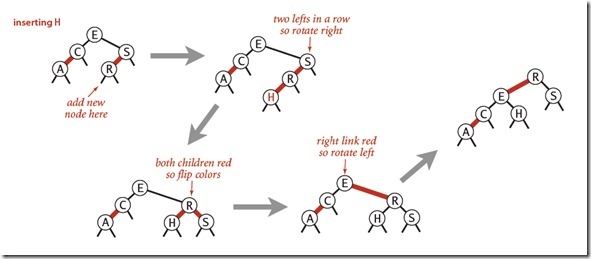
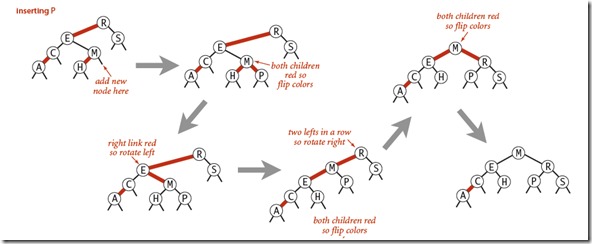
注意图14中到红色传递到根节点M后,由于根节点没有父节点,它的红黑属性不再重要,为了维持不打破上述的规则,定义根节点始终为黑. 如果通过颜色反转或者其他平衡化操作,把根节点变红以后,可以视作根节点还是黑.(强制根节点黑)

Put实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public override void Put(TKey key, TValue value)
{
    root = Put(root, key, value);
    root.Color = BLACK; // 强制根节点黑
}

private Node Put(Node h, TKey key, TValue value)
{
    if (h == null) return new Node(key, value, 1, RED);
    
    // 1. 进行二叉树插入: 
    int cmp = key.CompareTo(h.Key);
    if (cmp < 0) h.Left = Put(h.Left, key, value);
    else if (cmp > 0) h.Right = Put(h.Right, key, value);
    else h.Value = value;

    // 2. 进行平衡化:
    if (IsRed(h.Right) && !IsRed(h.Left)) h = RotateLeft(h); // 右边红节点
    if (IsRed(h.left) && IsRed(h.Left.Left)) h = RotateRight(h); // 我个人理解的写法,连续红节点
    // if (IsRed(h.Right) && IsRed(h.Left.Left)) h = RotateRight(h); //  原文写法,我感觉不对	
    if (IsRed(h.Left) && IsRed(h.Right)) h = FlipColor(h);// 颜色反转

    h.Number = Size(h.Left) + Size(h.Right) + 1; // 更新子树size信息
    return h;
}

private int Size(Node node)
{
    if (node == null) return 0;
    return node.Number;
}

注意到插入操作是自顶向下(dfs递归调用)进行的,由于dfs深度优先,可以先从子节点检查平衡/调整.因此不平衡从子节点传递到父节点,可以逐步调整传递到根节点,平衡操作也贯穿这个层层返回的过程,从平衡树的底层一直进行到根节点为止.

性能

满足上述规则后, 红黑树能保障所有操作最坏复杂度为O(logN)。

  • 最坏情况:
    除了最左侧路径,其他全部是3-node组成. 红黑相间的路径长度是全黑路径的两倍.

特性:
红黑树从根节点到叶子节点的路径中,全黑路径是平衡的.

应用

主要是各种map/符号表:

1
2
3
4
Java: TreeMap,TreeSet,HashMap,ConcurrentHashMap
C++: STL: map,multimap,multiset
.Net: SortedDictionary,SortedSet
Linux: epoll,防火墙规则表

核心规则

  1. 不能两个左右子节点都是红节点; (颜色反转)
  2. 父子节点不能都是红节点;(右旋)
  3. 右节点不能是红节点;(左旋)
  4. 新插入的节点是红节点;(新红)
  5. 根节点强制是黑节点.(根黑)

推荐文章