What: HLL/HyperLogLog是啥
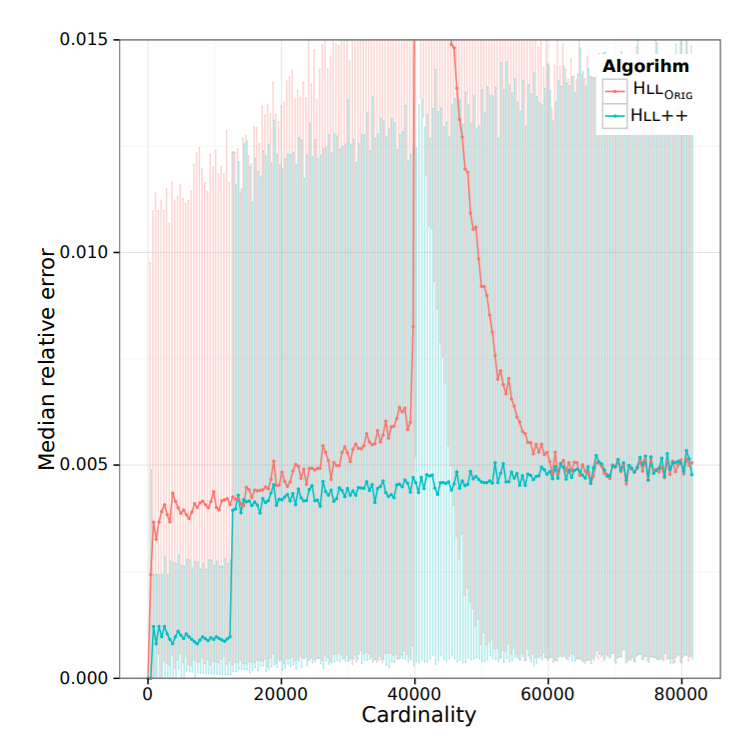
近似计算uv的算法,每一千万错误率0.5%.
谷歌改进后的算法为HLL++/HyperLogLog plus算法,改进了一些边界和精度问题(分类处理了稀疏和稠密的数据集情况,稀疏转化成稠密)。HLL++在边界条件下从1.5%优化到0.5%。而且不会出现突变高的错误率情况。
论文:
http://static.googleusercontent.com/media/research.google.com/en/us/pubs/archive/40671.pdf
How: HLL原理
n次伯努利
进行了n次进行抛硬币实验,每次分别记录下第一次抛到正面的抛掷次数K1~Kn,那么可以用n次实验中最大的抛掷次数Kmax;
则可以预估实验组数量为n的预估值=2^Kmax.
参考:
http://www.rainybowe.com/blog/2017/07/13/%E7%A5%9E%E5%A5%87%E7%9A%84HyperLogLog%E7%AE%97%E6%B3%95/index.html
LC算法
所有数据hash以后,从低位开始第一个1的位置K。
预估值为2^K.
HLL算法
分桶后求调和平均,概率上减少异常。
redis中的实现
代码:https://github.com/antirez/redis/blob/unstable/src/hyperloglog.c
内存: 2^14个桶,每个桶6bit。(实际作为一个大数组12KB。)
- 每个输入通过hash算法得出64bit哈希值x;
- x的低14位,用来选择桶号(0-2^14-1号)Mi;
- x的高50位,用来找K(也就是第一次出现1的位置,或者说0后缀的长度),把K存入Mi。
这样处理完所有用户输入后,用公式算出n的估计值:
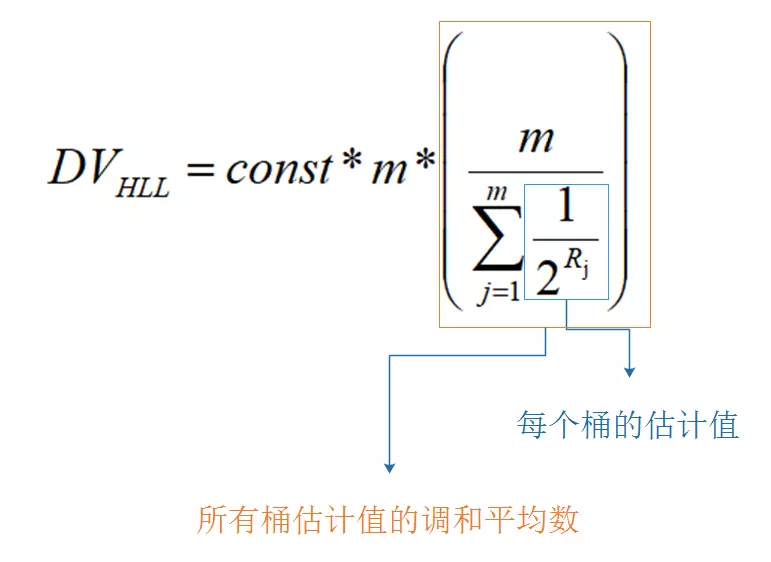
对于第三点中的K,(也就是n次伯努利里的Kmax) (对于每个用户id的Kmax值存入桶的6位中)
高位剩下50位,第一个1的位置最大是50,而2^6=64,所以能够存下50这个数字(以及其他所有Kmax)。
HLL++的话还要加入更多的边界调整。
可视化模拟
http://content.research.neustar.biz/blog/hll.html
上述链接中是m=64个桶(4*16的方阵),每个格子中存放一个十进制数,实际最大是2^6也就是64,如果新来了K值,则会和原来的K值做逻辑交运算。
